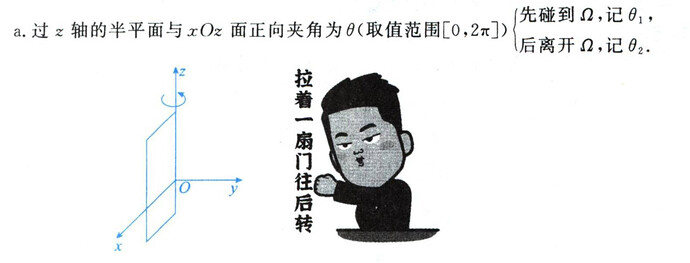
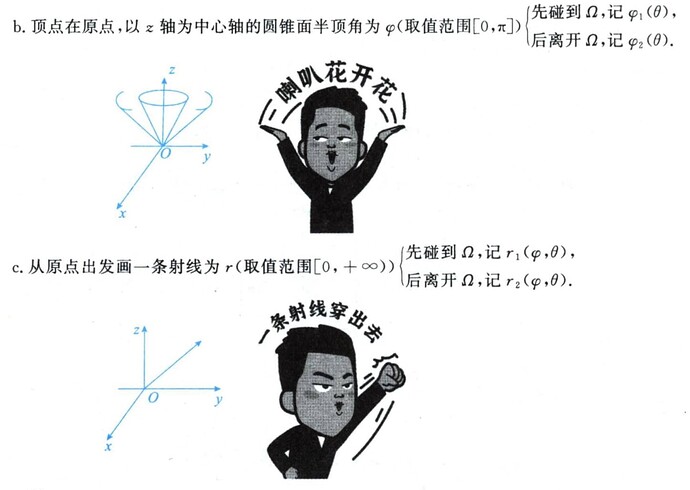
在球坐标系中,每个点的位置由三个坐标 (r, \theta, \phi) 确定,其中 r 表示从原点到点的径向距离, \theta 是方位角, \phi 是极角。应如何正确选择积分区间,以确保积分覆盖整个感兴趣的空间区域?
球坐标 (r, \theta, \phi) 的范围通常定义为:
- r\geq0: 半径,表示点到原点的距离。
- \theta\in[0,2\pi]:方位角,通常是在 xy-平面上从正 x 轴量起的角度。
- \phi\in[0,\pi]: 极角,从正 z-轴到点的直线与 z-轴之间的角度。
直角坐标与球面坐标的关系为:
\begin{cases}
x=r\sin\varphi\cos\theta,\\
y=r\sin\varphi\sin\theta,\\
z=r\cos\varphi.
\end{cases}
\begin{aligned} \iiint_{\Omega}f(x,y,z)\mathrm{d}v& =\iiint_{\Omega}f(r\sin\varphi\cos\theta,r\sin\varphi\sin\theta,r\cos\varphi)r^{2}\sin\varphi\mathrm{d}r\mathrm{d}\varphi\mathrm{d}\theta \\ &=\int_{\theta_1}^{\theta_2}\mathrm{d}\theta\int_{\varphi_1(\theta)}^{\varphi_2(\theta)}\mathrm{d}\varphi\int_{r_1(\varphi,\theta)}^{r_2(\varphi,\theta)}f(r\sin\varphi\cos\theta,r\sin\varphi\sin\theta,r\cos\varphi)r^2\sin\varphi\mathrm{d}r. \end{aligned}
参考资料:
- 张宇高等数学 18 讲